20  텐서(Tensor)

PyTorch의 기본 데이터 구조인 텐서(tensor)는 NumPy 배열을 확장한 형태로, 다차원 배열을 지원하고, GPU 가속(acceleration)을 통해 빠른 연산을 할 수 있도록 한다. PyTorch의 텐서는 다음과 같은 특징은 꼭 기억할 필요가 있다.

21 torch.tensor()로 텐서를 만들고 기본 정보 확인

보통 다음과 같은 방법으로 PyTorch를 임포트한다.

import torch

PyTorch 텐서를 생성하는 가장 기본적인 방법은 torch.tensor() 함수를 사용하는 것이다. 이 함수는 리스트나 NumPy 배열을 입력으로 받아 텐서를 생성한다. 다음 예제에서는 1차원, 2차원, 3차원 텐서를 생성하고, 각 텐서의 차원, 크기, 데이터 타입을 확인하는 방법을 보여준다. Numpy 패키지의 np.arrray()와 유사한 기능을 한다.

PyTorch 텐서와 Numpy 배열의 차이점

PyTorch 텐서와 Numpy 배열은 유사한 점이 많기는 하지만 다른 점들도 있다. API도 다를 수 있기 때문에 주의할 필요가 있다.

다음은 Python 값이나 리스트를 사용하여 텐서를 만드는 예로 다음을 주목하면서 살펴보자.

  • torch.tensor() 함수를 사용하여 텐서를 생성한다.
  • torch.tensor() 함수는 입력으로 Python 값이나 리스트를 받을 수 있다.
  • dtype 인자를 사용하여 텐서의 데이터 타입을 지정할 수 있다. 기본값은 torch.float32이다.
    • PyTorch는 디폴트로 32비트 부동소수점(float32) 타입을 사용한다는 점을 기억할 필요가 있다.
    • 그래서 torch.float는 torch.float32와 동일하다.
  • .ndim, .size(), .shape, .dtype 속성을 사용하여 텐서의 차원, 크기, 형태, 데이터 타입을 확인할 수 있다.
# 스칼라
scalar = torch.tensor(5)
scalar
tensor(5)
# 1차원 텐서 생성
tensor_1d = torch.tensor([1, 2, 3])
tensor_1d
tensor([1, 2, 3])
# 2차원 텐서 생성
tensor_2d = torch.tensor([[1, 2, 3], [4, 5, 6]])
tensor_2d
tensor([[1, 2, 3],
        [4, 5, 6]])
# 3차원 텐서 생성
tensor_3d = torch.tensor([[[1, 2], [3, 4]], [[5, 6], [7, 8]]])
tensor_3d
tensor([[[1, 2],
         [3, 4]],

        [[5, 6],
         [7, 8]]])

다음은 부동소수점 수를 사용한 2차원 텐서의 예이다.

float_tensor_2d = torch.tensor([[1.0, 2.0, 3.0], 
                                [4.0, 5.0, 6.0]])
print(float_tensor_2d.size())
print(float_tensor_2d.dtype)
torch.Size([2, 3])
torch.float32

텐서의 특징을 확인하는 방법이다. 어떤 경우에는 메서드(method)로, 어떤 경우에는 속성(attribute)으로 확인할 수 있다.

print("2차원 텐서 차원:", tensor_2d.dim())
print("2차원 텐서 차원:", tensor_2d.ndim)
print("2차원 텐서 크기:", tensor_2d.size())
print("2차원 텐서 형태:", tensor_2d.shape)
print("2차원 텐서 보폭:", tensor_2d.stride())
print("2차원 텐서 데이터 타입:", tensor_2d.dtype)
2차원 텐서 차원: 2
2차원 텐서 차원: 2
2차원 텐서 크기: torch.Size([2, 3])
2차원 텐서 형태: torch.Size([2, 3])
2차원 텐서 보폭: (3, 1)
2차원 텐서 데이터 타입: torch.int64

조금 더 눈여결 볼 것은 보폭(stride)이다. 보폭은 텐서의 각 차원에서 다음 요소로 이동하는 데 필요한 메모리 바이트 수를 나타낸다. 예를 들어, 2차원 텐서의 경우 첫 번째 차원(행)과 두 번째 차원(열)의 보폭을 확인할 수 있다. NumPy 배열에서는 np.ndarray.strides 속성을 사용하여 보폭을 확인할 수 있다. PyTorch에서는 .stride() 메서드를 사용한다. 또한 np.ndarray.strides는 그 값들을 바이트(byte) 단위로 반환하지만, PyTorch의 .stride() 메서드는 값의 개수를 반환한다.

tensor_2d
tensor([[1, 2, 3],
        [4, 5, 6]])
tensor_2d.stride()
(3, 1)

앞에서 본 것처럼 텐서의 데이터 타입은 .dtype 속성을 사용하여 확인할 수 있다. 데이터 타입을 변환하려면 type() 메서드를 사용할 수 있다. 예를 들어, torch.float64로 변환하려면 다음과 같이 한다. NumPy에서는 astype() 메서드가 이런 역할을 한다.

print("2차원 텐서 데이터 타입:", tensor_2d.dtype)
tensor_2d = tensor_2d.type(torch.float64)
print("바뀐 데이터 타입:", tensor_2d.dtype)
2차원 텐서 데이터 타입: torch.int64
바뀐 데이터 타입: torch.float64

21.1 텐서를 만드는 다양한 방법

torch.tensor() 함수 이외에도 다양한 상황에 맞춰 그에 합당한 텐서를 만들 수 있는 함수들이 있다. 즉, 선형대수 계산이나 딥러닝 모델을 만들 때 필요한 형태의 텐서를 쉽게 생성할 수 있도록 다양한 함수를 제공한다. 이들 함수는 텐서의 크기(shape), 데이터 타입(dtype), 초기값 등을 지정할 수 있는 인자를 제공한다.

다음은 자주 사용되는 텐서 생성 함수들이다.

21.1.1 난수를 사용하여 텐서 만들기

딥러닝 모델을 만들 때, 가중치 등을 난수를 사용하여 초기화하는 것이 일반적이다. PyTorch에서는 난수를 사용하여 텐서를 만드는 다양한 함수를 제공한다. 다음은 몇 가지 예시이다.

  • torch.rand() 함수는 0과 1 사이의 균등 분포에서 난수를 생성하여 텐서를 만든다.
  • torch.randint() 함수는 지정한 범위 안에 속하는 정수를 난수로 생성하여 텐서를 만든다.
  • torch.randn() 함수는 표준 정규 분포(평균 0, 표준편차 1)에서 난수를 생성한다.
  • torch.normal() 함수는 지정한 평균과 표준편차를 사용하여 정규 분포에서 난수를 생성한다.
# 0과 1 사이의 균등 분포에서 난수를 생성하여 2x3 텐서를 만든다.
uniform_tensor = torch.rand(2, 3)
uniform_tensor
tensor([[0.6977, 0.7780, 0.4635],
        [0.2095, 0.0480, 0.0638]])
# 0부터 9까지의 정수 중에서 난수를 생성하여 2x3 텐서를 만든다.
random_int_tensor = torch.randint(0, 10, (2, 3))
random_int_tensor
tensor([[7, 5, 1],
        [8, 2, 5]])
# 표준 정규 분포에서 난수를 생성하여 2x3 텐서를 만든다.
normal_tensor = torch.randn(2, 3)
normal_tensor
tensor([[-1.5302,  0.6437, -1.5196],
        [-0.4024,  1.2534,  0.6624]])
# 평균이 5, 표준편차가 2인 정규 분포에서 난수를 생성하여 2x3 텐서를 만든다.
mean = 5
std_dev = 2
normal_tensor_custom = torch.normal(mean, std_dev, size=(2, 3))
normal_tensor_custom
tensor([[7.8622, 0.3080, 4.5266],
        [4.4035, 5.1819, 4.7434]])

이들 함수 이름 뒤에 _like를 붙이면, 지정한 텐서와 동일한 크기(shape)를 갖는 텐서를 생성한다. 예를 들어, torch.rand_like(tensor)는 tensor와 동일한 크기의 텐서를 생성한다. 이들은 딥러닝 모델을 만들 때, 기존의 다른 텐서와 크기를 맞추면서 난수 값을 들어간 텐서를 만들 때 유용하게 사용된다.

tensor_2d 
tensor([[1., 2., 3.],
        [4., 5., 6.]], dtype=torch.float64)
# tensor_2d와 동일한 크기의 텐서를 생성한다.
rand_like_tensor = torch.rand_like(tensor_2d)
rand_like_tensor
tensor([[0.1353, 0.5759, 0.6341],
        [0.4019, 0.6046, 0.9602]], dtype=torch.float64)
# tensor_2d와 동일한 크기의 텐서를 생성한다.
randint_like_tensor = torch.randint_like(tensor_2d, 0, 10)
randint_like_tensor
tensor([[2., 6., 6.],
        [5., 4., 9.]], dtype=torch.float64)
# tensor_2d와 동일한 크기의 텐서를 생성한다.
randn_like_tensor = torch.randn_like(tensor_2d)
randn_like_tensor
tensor([[ 0.2358,  1.3932, -0.8122],
        [-2.2315, -1.4526,  0.4354]], dtype=torch.float64)
# tensor_2d와 동일한 크기의 텐서를 생성한다.
mean = 5
std_dev = 2
normal_like_tensor = torch.normal(mean, std_dev, size=tensor_2d.size())
normal_like_tensor
tensor([[7.5340, 1.0804, 9.7463],
        [5.3116, 4.8621, 4.6729]])

21.1.2 제로 텐서 만들기

PyTorch에서는 torch.zeros() 함수를 사용하여 제로 텐서를 생성할 수 있다. 이 함수는 모든 값이 0인 지정한 크기의 텐서를 생성한다.

# 2x3 크기의 제로 텐서를 생성한다.
zero_tensor = torch.zeros(2, 3)
zero_tensor
tensor([[0., 0., 0.],
        [0., 0., 0.]])

이 경우에도 _like를 붙이면, 지정한 텐서와 동일한 크기의 제로 텐서를 생성할 수 있다.

# tensor_2d와 동일한 크기의 제로 텐서를 생성한다.
zero_like_tensor = torch.zeros_like(tensor_2d)
zero_like_tensor
tensor([[0., 0., 0.],
        [0., 0., 0.]], dtype=torch.float64)

21.1.3 1로 구성된 텐서 만들기

PyTorch에서는 torch.ones() 함수를 사용하여 온 텐서를 생성할 수 있다. 이 함수는 모든 값이 1인 지정한 크기의 텐서를 생성한다.

# 2x3 크기의 온 텐서를 생성한다.
one_tensor = torch.ones(2, 3)
one_tensor
tensor([[1., 1., 1.],
        [1., 1., 1.]])

이 경우에도 _like를 붙이면, 지정한 텐서와 동일한 크기의 텐서를 생성할 수 있다.

# tensor_2d와 동일한 크기의 온 텐서를 생성한다.
one_like_tensor = torch.ones_like(tensor_2d)
one_like_tensor
tensor([[1., 1., 1.],
        [1., 1., 1.]], dtype=torch.float64)

21.1.4 단위 행렬 만들기

PyTorch에서는 torch.eye() 함수를 사용하여 단위 행렬(identity matrix)을 생성할 수 있다. 단위 행렬은 주대각선의 원소가 모두 1이고, 나머지 원소는 모두 0인 정사각행렬이다.

# 3x3 단위 행렬 생성
identity_matrix = torch.eye(3)
identity_matrix
tensor([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])
# 4x4 단위 행렬 생성
identity_matrix_4x4 = torch.eye(4)
identity_matrix_4x4
tensor([[1., 0., 0., 0.],
        [0., 1., 0., 0.],
        [0., 0., 1., 0.],
        [0., 0., 0., 1.]])

21.1.5 대각 행렬 만들기

대각 행렬(diagonal matrix)은 주대각선의 원소만 0이 아니고, 나머지 원소는 모두 0인 행렬이다. PyTorch에서는 torch.diag() 함수를 사용하여 대각 행렬을 생성할 수 있다.

# 1차원 텐서를 사용하여 대각 행렬 생성
diagonal_tensor = torch.tensor([1, 2, 3])
diagonal_matrix = torch.diag(diagonal_tensor)
diagonal_matrix
tensor([[1, 0, 0],
        [0, 2, 0],
        [0, 0, 3]])
# 2차원 텐서를 사용하여 대각 행렬 생성
diagonal_tensor_2d = torch.tensor([[1, 2], [3, 4]])
diagonal_matrix_2d = torch.diag(diagonal_tensor_2d)
diagonal_matrix_2d
tensor([1, 4])

21.1.6 Numpy 배열로 텐서 만들기

torch.from_numpy() 함수를 사용하여 NumPy 배열을 PyTorch 텐서로 변환할 수 있다. 이 함수는 NumPy 배열의 메모리를 공유하는 텐서를 생성한다. 즉, NumPy 배열과 PyTorch 텐서는 동일한 메모리 공간을 사용하므로 메모리를 효율적으로 사용할 수 있다. 하지만 NumPy 배열이 변경되면 PyTorch 텐서도 변경되므로 주의할 필요가 있다.

import numpy as np
# NumPy 배열 생성
numpy_array = np.array([[1, 2, 3], [4, 5, 6]])
# NumPy 배열을 PyTorch 텐서로 변환
tensor_from_numpy = torch.from_numpy(numpy_array)
tensor_from_numpy
tensor([[1, 2, 3],
        [4, 5, 6]])

21.2 텐서가 메모리에 저장되는 방식과 관련 개념들

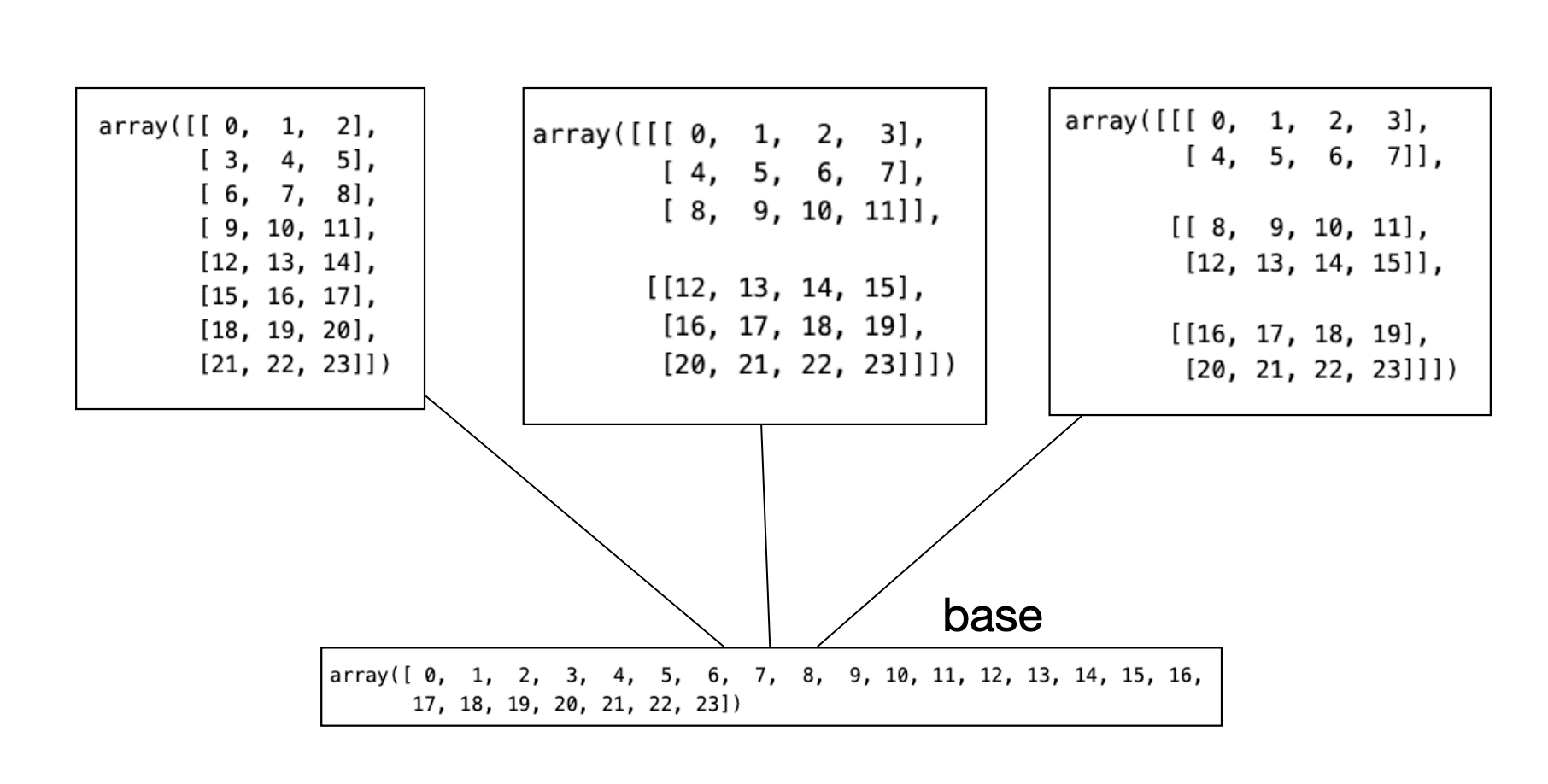
PyTorch 텐서가 메모리에 저장되는 방식은 섹션 17.3에서 설명했던 NumPy 배열과 거의 같다. 물론 내부적으로 구현은 다르겠지만, 전체적인 개념은 유사하다. 넘파이에서는 다음 그림과 같은 비유를 사용했었다.

그림 21.1: 왼쪽은 뱀 큐브가 1차원적으로 배열된 모습을 오른쪽은 뱀 큐브로 만든 형태들을 보여준다. 메모리에 1차원적으로 저장된 값들을 가지고 stride 등의 값을 바꿔서 메모리를 공유하면서도 모양이 다른 뷰 텐서들을 만들 수 있다.
그림 21.2: NumPy에서는 base라고 하고 PyTorch에서는 Storage라고 한다. 모두 파생된 배열을 뷰(views)라고 한다.

  • 연속성(Contiguity): PyTorch 텐서는 기본적으로 연속적인 메모리 블록에 저장된다. 즉, 텐서의 모든 요소가 메모리 상에서 연속적으로 배치된다. 이는 CPU와 GPU에서 빠른 연산을 가능하게 한다.

  • 데이터 타입: PyTorch 텐서는 한 가지 데이터 타입만을 가질 수 있다. 즉, 텐서의 모든 요소는 동일한 데이터 타입을 갖는다. 이는 메모리 사용을 최적화하고, 연산 속도를 향상시킨다.

  • 메모리 공유: 뷰(View) 텐서를 사용하면, 기존 텐서의 메모리를 공유하면서 서로 다른 텐서들을 만들 수 있다. 보폭(stride)을 조정하여 텐서의 모양을 변경할 수 있다. 대표적인 예가 torch.reshape(), torch.view() 함수 또는 torch.transpose() 함수이다. 이들 함수는 원본 텐서의 메모리를 그대로 사용하면서, 새로운 모양의 텐서를 생성한다. torch.fron_numpy() 함수도 NumPy 배열의 메모리를 공유하는 텐서를 생성하는 예를 보았는데, 이처럼 메모리를 효율적으로 사용할 수 있는 장치가 잘 마련되어 있다.

NumPy 배열에서는 base 속성을 사용하여 메모리 공유를 확인할 수 있지만, PyTorch에서는 base 속성이 없다. 대신, Stroge 객체를 사용하여 텐서의 메모리 정보를 확인할 수 있다. 이와 같은 기본 개념을 이해하면 아래 내용들을 좀 더 쉽게 이해할 수 있다.

21.2.1 in-place 연산: 메모리의 값을 직접 수정

PyTorch에서는 in-place 연산을 지원하여, Storage에 있는 텐서의 값을 직접 수정할 수 있다. in-place 연산은 메모리 사용을 최적화하고, 불필요한 메모리 할당을 줄이는 데 유용하다. in-place 연산은 함수 이름 뒤에 _가 붙는다. 예를 들어, tensor.add_(value)는 tensor의 값을 value만큼 더하는 in-place 연산이다. 또 tensor.zero_()는 tensor의 값을 모두 0으로 설정하는 in-place 연산이다.

# 텐서 생성
tensor = torch.tensor([1, 2, 3])
# in-place 연산: 텐서의 값을 10으로 변경
tensor.add_(10)
tensor
tensor([11, 12, 13])
tensor = torch.tensor([1, 2, 3])
# in-place 연산: 텐서의 값을 모두 0으로 변경
tensor.zero_()
tensor
tensor([0, 0, 0])
in-place 연산 사용 시 주의사항
  • 자동 미분(autograd): in-place 연산은 자동 미분에 영향을 줄 수 있다. 특히, in-place 연산을 사용한 후에는 그래디언트 계산이 제대로 이루어지지 않을 수 있다. 따라서, 자동 미분을 사용하는 경우에는 in-place 연산을 피하는 것이 좋다.
  • 가독성: in-place 연산을 사용한 후에는 원래 텐서의 값을 알 수 없기 때문에, 코드의 이해가 어려워질 수 있다.

21.2.2 인덱싱과 슬라이싱

PyTorch 텐서에서는 NumPy와 유사한 방식으로 인덱싱(indexing)과 슬라이싱(slicing)을 지원한다. 이를 통해 텐서의 특정 요소나 부분을 선택할 수 있다. 인덱싱과 슬라이싱은 텐서의 모양(shape)을 변경하지 않고, 텐서의 일부를 참조하는 뷰(view)를 생성한다.

# 2차원 텐서 생성
tensor_2d = torch.tensor([[1, 2, 3], [4, 5, 6]])
# 첫 번째 행 선택
first_row = tensor_2d[0]
first_row
tensor([1, 2, 3])
# 두 번째 열 선택
second_column = tensor_2d[:, 1]
second_column
tensor([2, 5])
# 첫 번째 행과 두 번째 열 선택
first_row_second_column = tensor_2d[0, 1]
first_row_second_column
tensor(2)

21.3 자동 미분(Autograd)

PyTorch의 자동 미분(autograd) 기능은 신경망 모델을 학습할 때 매우 유용하다. 자동 미분은 텐서의 연산을 추적하고, 그라디언트를 자동으로 계산하는 기능이다. 자동 미분을 사용하려면, 텐서를 생성할 때 requires_grad=True로 설정해야 한다. 이렇게 하면 해당 텐서에 대한 모든 연산이 추적되고, 그라디언트를 계산할 수 있다.

아래 예제에서 x는 requires_grad=True로 설정되어 있어서 x에 값을 사용하는 연산은 내부에서 computational graph로 추적하다. 그래서 마지막 결과인 y에 대해 y.backward()를 호출하면 y를 x로 미분한 결과가 x의 .grad 속성에 저장된다.

x = torch.tensor(2.0, requires_grad=True)
y = x ** 2 + 3 * x + 1
y.backward()  # dy/dx 자동 계산
print(x.grad)  # 출력: 7.0
tensor(7.)

신경망 모델의 가중치와 편향을 정의하고 이 텐서들에 대해 requires_grad=True로 설정하면, 모델의 출력에 대한 손실(loss)을 계산한 후 loss.backward()를 호출하여 가중치와 편향에 대한 그라디언트가 가중치와 편향의 .grad 속성에 저장된다. 이렇게 저장된 그라디언트는 옵티마이저(optimizer)를 사용하여 가중치와 편향을 업데이트하는 데 사용된다.

Autograd 정리
  • 추적할 변수에 대한 텐서를 requires_grad=True로 설정한다.
  • 해당 변수를 사용한 연사들을 추적하여 computational graph를 만든다.
  • 최종 결과를 담은 텐서에 대해 .backward() 메서드를 호출한다.
  • .backward() 메서드는 자동으로 그래디언트를 계산하고, 추적된 텐서의 .grad 속성에 저장한다.

그럼 텐서의 연산을 추적한다는 의미에 대해서 살펴보자. PyTorch는 텐서의 연산을 추적하여 computational graph를 생성한다. 이 그래프는 각 텐서와 그 텐서에 대한 연산을 노드로 표현하며, 연산의 순서를 나타낸다. 이 그래프를 사용하여 자동으로 그라디언트(기울기)를 계산할 수 있다.

딥러닝에서 경사 하강법(Gradient Descent)라는 방법을 사용하여 파라미터를 최소화한다. 이것은 손실 함수(loss function)를 최소화하기 위해서 어느 지점에서 손실 함수의 파라미터에 대한 그라디언트를 계산하여, 이 기울기를 보고 파라미터를 어떻게 업데이트할지 결정한다.

21.3.1 Computational Graph (연산 그래프)

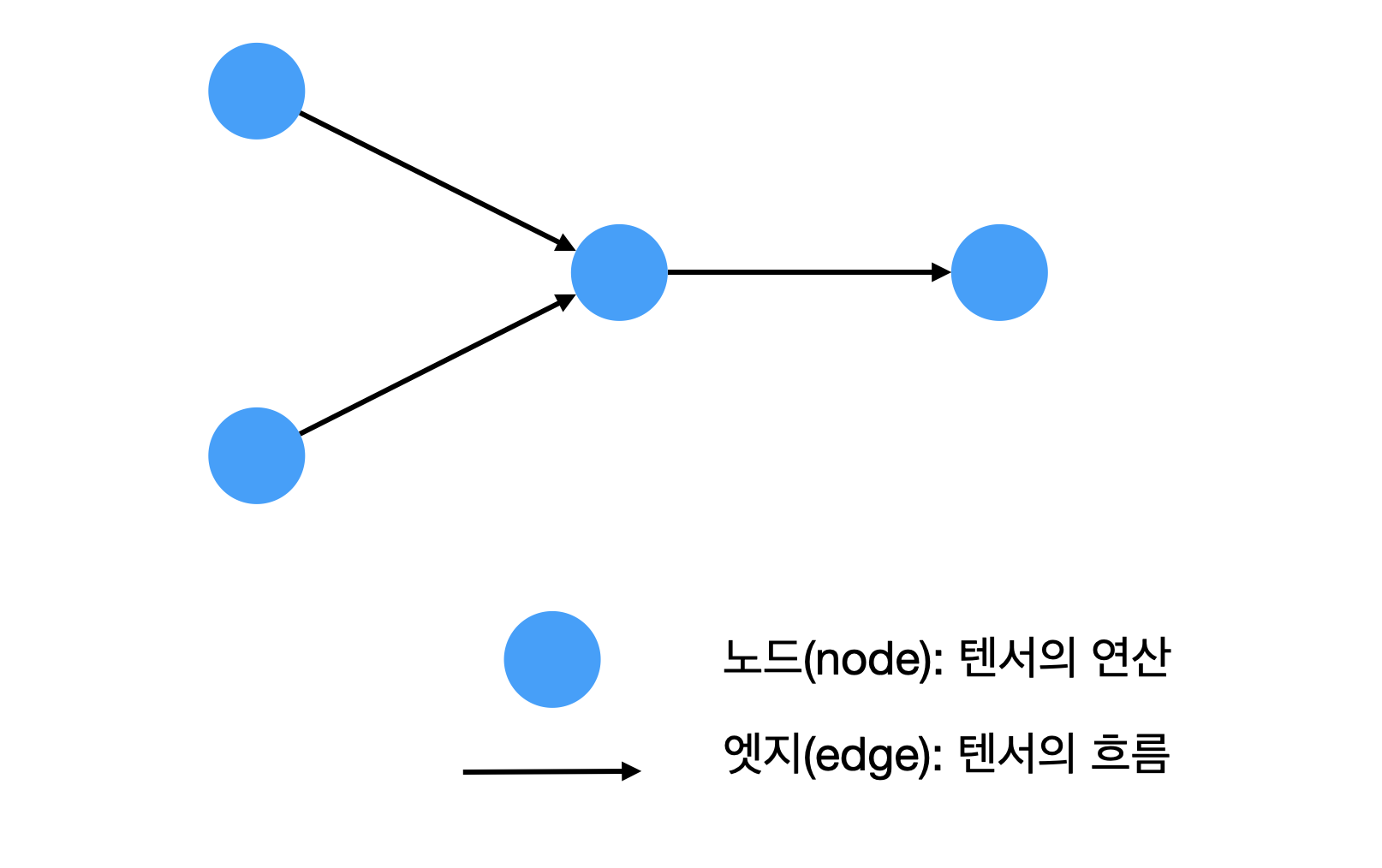
여기서 말하는 컴퓨테이셔널 그래프(computational graph)에서 그래프는 통상 이야기는 플롯이 아니고, 그래프 이론에서 말하는 그래프이다. 컴퓨테이셔널 그래프는 연산을 노드로 표현하고, 노드 간의 관계를 엣지(edge)로 표현한 그래프이다.

그림 21.3: 컴퓨테이셔널 그래프

다음 수식을 예로 보자.

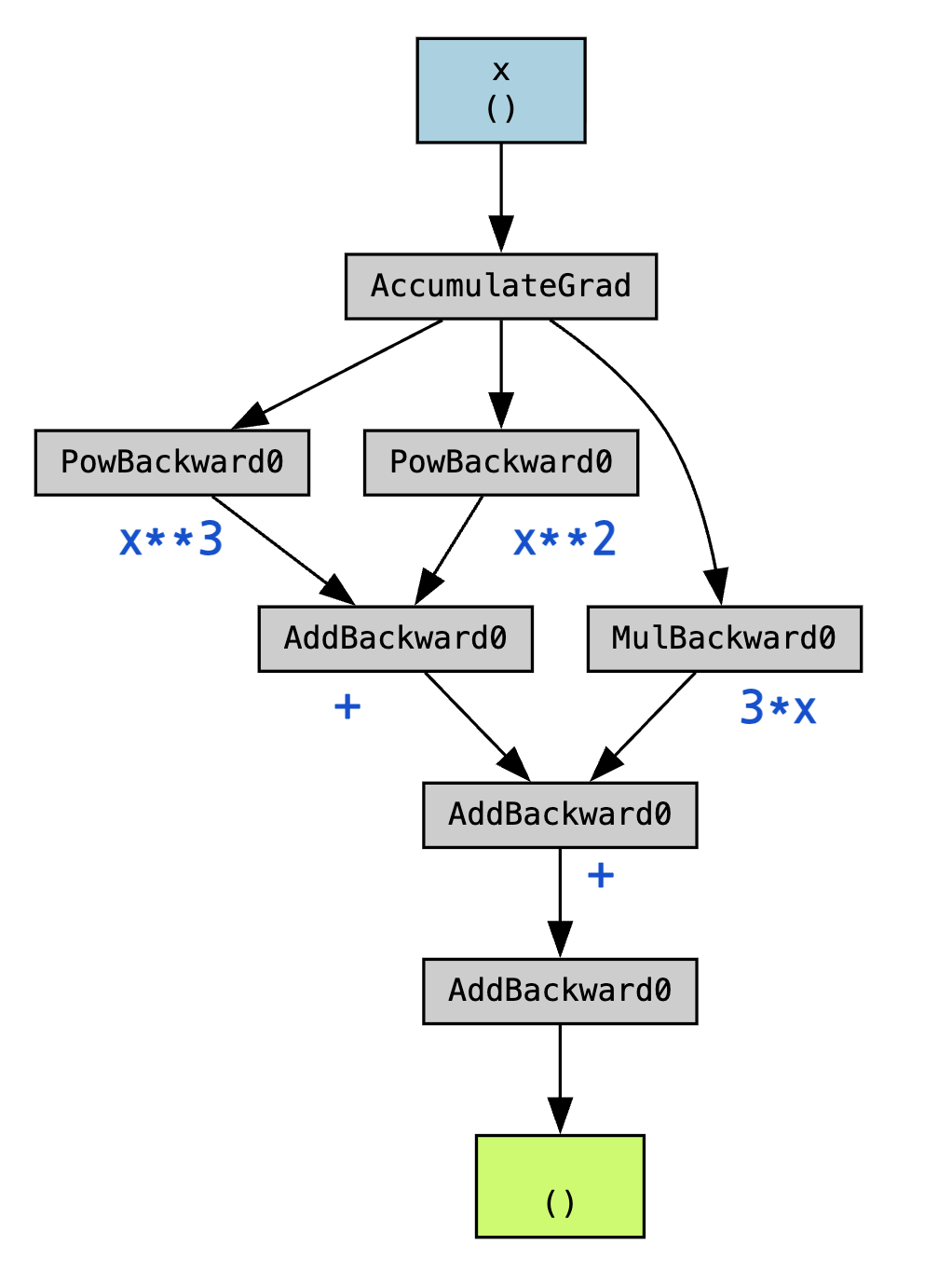
\[ y = x^3 + x^2 + 3x + 1 \]

이 수식을 컴퓨테이셔널 그래프로 표현하면 다음과 같다. 다음은 torchviz 패키지를 사용하여 연산 그래프를 시각화한 예이다. torchviz는 PyTorch의 연산 그래프를 시각화하는 데 유용한 도구이다.

import torch
# 텐서 생성
x = torch.tensor(2.0, requires_grad=True)
# 연산 수행
y = x**3 + x ** 2 + 3 * x + 1 
# 연산 그래프 시각화
from torchviz import make_dot
make_dot(y, params={"x": x})
그림 21.4: torchiz 패키지를 사용한 컴퓨테이셔널 그래프 시각화

좀 풀어서 보면 다음과 같다.

그림 21.5: 풀어서 본 컴퓨테이셔널 그래프: 노드는 연산을, 엣지는 흐름을 나타낸다.

이 예에서 연산의 흐름을 추적한다는 의미는 x에서 시작하여 y까지의 연산을 추적한다는 것이다. 즉, x에서 x^2, x^3, 3x, 1로 가는 경로를 따라가며 각 연산을 수행한다.

21.3.2 그라디언트(Gradient): 기울기와 최솟값

직관적으로 보았을 때 그라디언트는 함수의 기울기이고, 딥러닝은 어떤 함수의 최솟값을 찾아가는 과정이다. 다음 간단한 예를 보자.

\[ y = x^2 + 3x + 1 \]

고등학교 수학을 떠올려 보면, 이 함수는 아래로 볼록한 포물선 형태를 가지고 있다. 이 함수의 최솟값을 찾기 위해서는 기울기를 계산하여, 기울기가 0이 되는 지점을 찾아야 한다. 그렇게 하려면 미분을 해서 기울기를 계산하여야 한다.

이 함수의 기울기를 계산하면 다음과 같다. \[ \frac{dy}{dx} = 2x + 3 \] 이 기울기가 0이 되는 지점을 찾으면, 함수의 최솟값을 찾을 수 있다. 즉, \[ 2x + 3 = 0\] 에서 x를 구하면, \(x = -\frac{3}{2}\)가 된다. 이 값을 원래 함수에 대입하면 최솟값을 찾을 수 있다. \[ y = \left(-\frac{3}{2}\right)^2 + 3\left(-\frac{3}{2}\right) + 1 = -\frac{5}{4} \]

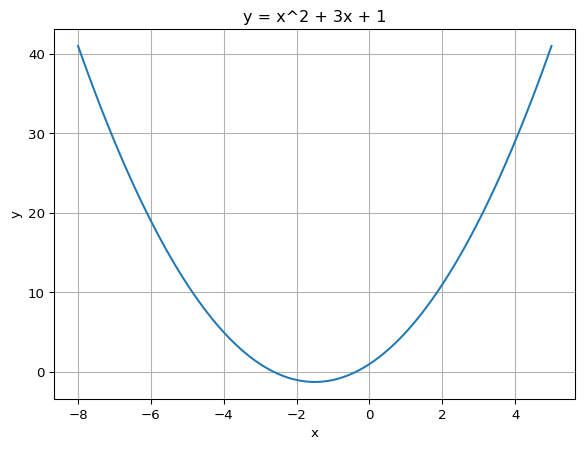
이 함수를 matplotlib 패키지를 사용하여 시각화하면 다음과 같다.

import matplotlib.pyplot as plt
import numpy as np
# x 값 생성

x_values = np.linspace(-8, 5, 100)
# y 값 계산
y_values = x_values**2 + 3*x_values + 1
# 그래프 그리기
fig, ax = plt.subplots()
ax.plot(x_values, y_values)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('y = x^2 + 3x + 1')
ax.grid(True)
plt.show()

이 그래프에서 \(x=-3\)에서의 기울기를 구하고 그래프로 표현해 보자. 이 기울기는 \(2x + 3\)에서 \(x=-3\)을 대입하여 구할 수 있다. 즉, \(2(-3) + 3 = -6 + 3 = -3\)이 된다. 이 기울기를 사용하여 접선을 그려보자.

# 기울기를 그리기 위한 x 값
x_tangent = -3
# 기울기 계산
slope = 2 * x_tangent + 3
# y 값 계산
y_tangent = x_tangent**2 + 3*x_tangent + 1
# 그래프 그리기
fig, ax = plt.subplots()
ax.plot(x_values, y_values, label='y = x^2 + 3x + 1')
ax.plot(x_tangent, y_tangent, 'ro')  # 기울기 점
ax.plot(x_values, slope * (x_values - x_tangent) + y_tangent, label='Tangent Line', color='orange')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Tangent Line at x = -3')
ax.grid(True)
ax.legend()
plt.show()
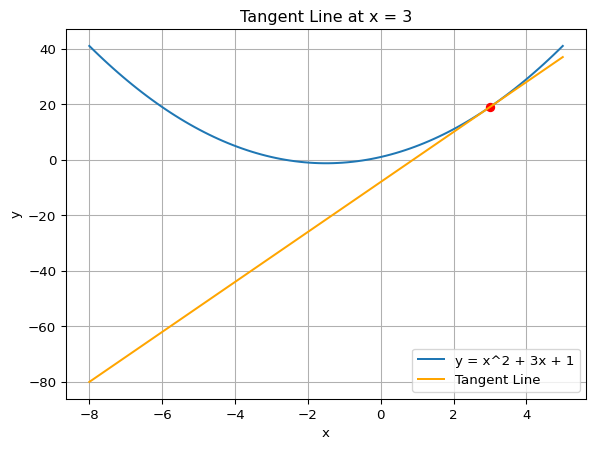
그림 21.6: \(x=-3\)에서의 기울기가 음수이기 때문에 최솟값을 찾기 위해서는 \(x\)를 오른쪽으로 이동해야 한다.

반면 이번에는 \(x=3\)에서의 기울기를 구하고 그래프로 표현해 보자. 이 기울기는 \(2x + 3\)에서 \(x=3\)을 대입하여 구할 수 있다. 즉, \(2(3) + 3 = 6 + 3 = 9\)이 된다. 이 기울기를 사용하여 접선을 그려보자.

# 기울기를 그리기 위한 x 값
x_tangent = 3
# 기울기 계산
slope = 2 * x_tangent + 3
# y 값 계산
y_tangent = x_tangent**2 + 3*x_tangent + 1
# 그래프 그리기
fig, ax = plt.subplots()
ax.plot(x_values, y_values, label='y = x^2 + 3x + 1')
ax.plot(x_tangent, y_tangent, 'ro')  # 기울기 점
ax.plot(x_values, slope * (x_values - x_tangent) + y_tangent, label='Tangent Line', color='orange')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('Tangent Line at x = 3')
ax.grid(True)
ax.legend()
plt.show()
그림 21.7: \(x=3\)에서의 기울기가 양수이기 때문에 최솟값을 찾기 위해서는 \(x\)를 왼쪽으로 이동해야 한다.

대체로 이와 같은 방식으로 딥러닝 모델의 파라미터를 업데이트한다. 즉, 손실 함수의 파라미터에 대한 그라디언트를 계산하고, 이 기울기를 보고 파라미터를 어떻게 업데이트할지 결정한다. 여기에 더 복잡한 수학이나 알고리즘이 사용되지만 기본적인 개념은 이렇다. 그림으로 배우는 딥러닝 책이 이 개념을 아주 잘 설명하고 있다(Glassner, 김창엽, and 소재현 2022).

21.3.3 체인 규칙(Chain Rule)과 역전파(Backpropagation)

미적분에서 체인 규칙(Chain Rule)이란 미분가능한 합성 함수의 미분에 적용되는 규칙이다. 합성 함수란 두 개 이상의 함수를 연결하여 만든 함수이다. 체인 규칙은 합성 함수의 미분을 구할 때, 각 함수의 미분을 곱하는 방식으로 계산한다.

\[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} \]

함수가 3개 이상인 경우도 마찬가지 규칙이 적용된다. \[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dv} \cdot \frac{dv}{dx} \]

이 규칙을 사용하면 복잡한 함수 미분도 간단해 질 수 있다. 예를 들어 다음과 같은 함수를 미분한다고 생각하자.

\[ y = \sin(x^2) \]

이것을 \(u=x^2\)라고 하면 다음과 같이 된다.

\[ y = \sin(u) \]

그래서 \(dy/du\)를 구하면 다음과 같다.

\[ \frac{dy}{du} = \cos(u) \]

그리고 \(du/dx\)를 구하면 다음과 같다.

\[ \frac{du}{dx} = 2x \]

그래서 체인 규칙을 적용하면 다음과 같이 된다.

\[ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = \cos(u) \cdot 2x = 2x \cos(x^2) \]

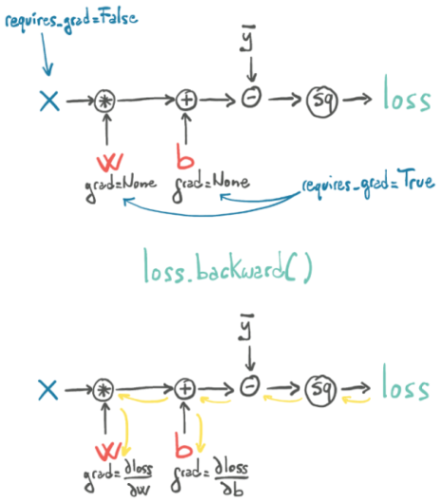
이 체인 규칙을 딥러닝 모델의 역전파(backpropagation) 알고리즘에 적용한다. 역전파는 신경망의 출력에서 입력으로 거슬러 올라가면서 각 가중치와 편향에 대한 그라디언트를 계산하는 과정이다. 이 과정은 체인 규칙을 사용하여 각 층의 가중치와 편향에 대한 그라디언트를 계산한다. 그림 21.8은 어느 책에서 인용한 그림인데, 역전파의 과정을 잘 보여준다.

그림 21.8: 파이토치 딥러닝 마스터에서 인용(Stevens et al. 2022)

딥러닝의 경우에는 마지막 결과가 손실 함수로 결정된다. 그리고 가중치와 편향에 대해 requires_grad=True로 설정되어 있다면, 이 값들이 여러 층이 만드는 함수를 통과하게 되어 결국 손실 함수에 이르게 된다. 이 손실 함수의 출력에 대해 backward() 메서드를 호출하면, PyTorch는 자동으로 역전파를 수행하여, 텐서가 연산 과정을 기억하고 있기 때문에, 역으로 그 과정을 추적해 갈 수 있다. 그리하여 체인 규칙에 따라 각 가중치와 편향에 대한 그라디언트를 계산한다. 계산된 값은 원래의 텐서의 .grad 속성에 저장된다. 다음 옵티마이저(optimizer)가 이 값을 사용하여 가중치와 편향을 업데이트한다.

21.4 GPU로 이동시키기

NumPy ndarray는 컴퓨터 CPU 메모리에서만 계산을 할 수 있다. 반면 PyTorch 텐서는 CPU와 GPU에서 모두 사용할 수 있다. (내가 사용하는) Apple Silicon Mac에서는 GPU 대신 Metal Performance Shaders(MPS)를 사용하여 GPU 가속을 지원한다. MPS 디바이스는 "mps"로 지정한다. torch.device를 사용하여 디바이스를 지정할 수 있다.

다음은 MPS 디바이스가 사용 가능한지 확인하는 방법이다.

torch.mps.is_available()
True

PyTorch에서는 torch.device를 사용하여 디바이스를 지정할 수 있다. 예를 들어, MPS 디바이스를 사용하려면 다음과 같이 지정한다.

device = torch.device("mps")
GPU와 CPU의 차이점

  • CPU: 일반적인 컴퓨팅 작업을 처리하도록 설계된 프로세서입니다. 복잡한 연산을 빠르게 처리할 수 있도록 고성능의 코어를 소수 포함하고 있습니다. 주로 운영 체제, 애플리케이션 실행, 데이터 처리 등 다양한 작업을 수행합니다.

  • GPU: 대량의 데이터를 병렬로 처리하도록 설계된 프로세서입니다. 수천 개의 작은 코어를 포함하고 있어, 대규모 병렬 연산에 적합합니다. 주로 그래픽 렌더링, 이미지 및 비디오 처리, 머신 러닝 및 딥러닝 작업에 사용됩니다.

torch.tensor()를 사용하여 텐서를 생성할 때, device 인자를 사용하여 디바이스를 지정할 수 있다. 예를 들어, MPS 디바이스에서 텐서를 생성하려면 다음과 같이 한다.

# MPS 디바이스에서 텐서 생성
t1 = torch.tensor([1, 2, 3], device=device)
t1
tensor([1, 2, 3], device='mps:0')

CPU 디바이스에 있는 텐서를 MPS 디바이스로 이동하려면 to() 메서드를 사용한다. 예를 들어, CPU 디바이스에 있는 텐서를 MPS 디바이스로 이동하려면 다음과 같이 한다.

# CPU 디바이스에 있는 텐서 생성
t2 = torch.tensor([4, 5, 6])
# MPS 디바이스로 이동
t2_mps = t2.to(device)
t2_mps
tensor([4, 5, 6], device='mps:0')
그림 21.9: Apple Silicon M1: 8-Core GPU를 가지고 있음

21.4.1 MPS 디바이스에서 MNIST 데이터셋 학습하기

mps 디바이스에서 torchvision에 포함된 MNIST 데이터셋을 다운로드하여 신경망을 학습하는 예제를 살펴보자.

import torch
import torchvision.transforms as transforms
from torchvision.datasets import MNIST
# MPS 디바이스 설정
device = torch.device("mps" if torch.backends.mps.is_available() else "cpu")
# MNIST 데이터셋 다운로드
mnist_train = MNIST(root='./data', train=True, download=True, transform=transforms.ToTensor())
mnist_test = MNIST(root='./data', train=False, download=True, transform=transforms.ToTensor())
# 데이터셋의 크기 확인
print(f"Train dataset size: {len(mnist_train)}")
print(f"Test dataset size: {len(mnist_test)}")
# 데이터셋의 첫 번째 이미지와 라벨 확인
image, label = mnist_train[0]
print(f"Image shape: {image.shape}, Label: {label}")
Train dataset size: 60000
Test dataset size: 10000
Image shape: torch.Size([1, 28, 28]), Label: 5
# MNIST 데이터셋의 첫 번째 이미지 시각화
import matplotlib.pyplot as plt
plt.imshow(image.squeeze(), cmap='gray')
plt.title(f"Label: {label}")
plt.axis('off')
plt.show()

# 신경망 모델 정의
import torch.nn as nn
class SimpleNN(nn.Module):
    def __init__(self):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(28 * 28, 128)
        self.fc2 = nn.Linear(128, 10)

    def forward(self, x):
        x = x.view(-1, 28 * 28)  # Flatten the input
        x = torch.relu(self.fc1(x))
        x = self.fc2(x)
        return x


# 모델 인스턴스 생성 및 MPS 디바이스로 이동
model = SimpleNN().to(device)

# 손실 함수와 옵티마이저 정의
criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 데이터로더 정의
from torch.utils.data import DataLoader
train_loader = DataLoader(mnist_train, batch_size=64, shuffle=True)
test_loader = DataLoader(mnist_test, batch_size=64, shuffle=False)
# 모델 학습 함수
def train(model, train_loader, criterion, optimizer, device):
    model.train()
    for images, labels in train_loader:
        images, labels = images.to(device), labels.to(device)
        optimizer.zero_grad()  # 기울기 초기화
        outputs = model(images)  # 모델 예측
        loss = criterion(outputs, labels)  # 손실 계산
        loss.backward()  # 역전파
        optimizer.step()  # 가중치 업데이트
# 모델 학습
num_epochs = 5
for epoch in range(num_epochs):
    train(model, train_loader, criterion, optimizer, device)
    print(f"Epoch [{epoch+1}/{num_epochs}] completed.")
Epoch [1/5] completed.
Epoch [2/5] completed.
Epoch [3/5] completed.
Epoch [4/5] completed.
Epoch [5/5] completed.
# 모델 평가 함수
def evaluate(model, test_loader, device):
    model.eval()
    correct = 0
    total = 0
    with torch.no_grad():
        for images, labels in test_loader:
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            _, predicted = torch.max(outputs.data, 1)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    accuracy = 100 * correct / total
    return accuracy
# 모델 평가
accuracy = evaluate(model, test_loader, device)
print(f"Test Accuracy: {accuracy:.2f}%")
Test Accuracy: 97.40%

이제 추론을 해 보자. 테스트 데이터셋에서 첫 번째 이미지를 사용하여 모델의 예측을 확인한다.

# 테스트 데이터셋에서 첫 번째 이미지 가져오기
test_image, test_label = mnist_test[0]
# 이미지를 MPS 디바이스로 이동
test_image = test_image.to(device)
# 모델을 평가 모드로 설정
model.eval()
# 예측 수행
with torch.no_grad():
    output = model(test_image.unsqueeze(0))  # 배치 차원 추가
    _, predicted_label = torch.max(output, 1)
print(f"Predicted Label: {predicted_label.item()}, Actual Label: {test_label}")
# 테스트 이미지 시각화
plt.imshow(test_image.squeeze().cpu(), cmap='gray')
plt.title(f"Predicted: {predicted_label.item()}, Actual: {test_label}")
plt.axis('off')
plt.show()  
Predicted Label: 7, Actual Label: 7

21.5 정리

PyTorch 텐서는 NumPy 배열과 유사한 방식으로 다차원 배열을 표현할 수 있는 강력한 도구이다. PyTorch 텐서는 자동 미분, GPU 가속, 다양한 연산 지원 등 딥러닝 모델을 구현하는 데 필요한 기능을 제공한다. PyTorch의 텐서를 이해하고 활용하는 것은 딥러닝 모델을 효과적으로 개발하고 학습시키는 데 매우 중요하다.